Question:
Sort a linked list using insertion sort.
Thinking:
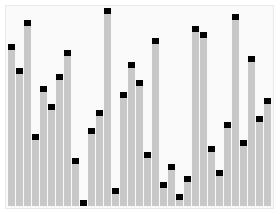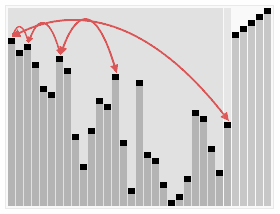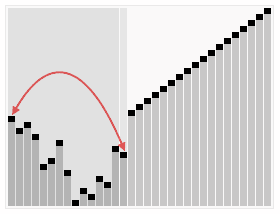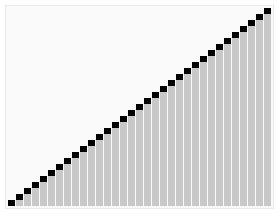
As the question state, we should apply the insertion sort method to linked list. So we create a ListNode for hold the sorted list, and scan the unsorted list and pick up element to compare the element in the sorted list. Then determine when to insert the value.
Solution:
public class Solution {
public ListNode insertionSortList(ListNode head) {
if (head == null || head.next == null)
return head;
ListNode res = new ListNode(-1);
res.next = head;
ListNode p = res;
ListNode next = head.next;
head.next = null;
head = next;
while (head != null){
while (p.next != null){
//if the value is smaller than one of the sorted list, insert behind it
if (head.val < p.next.val){
next = head.next;
head.next = p.next;
p.next = head;
head = next;
p = res;
break;
}
p = p.next;
}
//if the value is bigger than anyone of the sorted list, insert after the whole list
if (p.next == null){
next = head.next;
p.next = head;
head.next = null;
head = next;
p = res;
}
}
return res.next;
}
}
I also copy a refining version of this algorithm from reference: http://www.cnblogs.com/springfor/p/3862468.html
public ListNode insertionSortList(ListNode head) {
if(head == null||head.next == null)
return head;
ListNode sortedlisthead = new ListNode(0);
ListNode cur = head;
while(cur!=null){
ListNode next = cur.next;
ListNode pre = sortedlisthead;
while(pre.next!=null && pre.next.val<cur.val)
pre = pre.next;
cur.next = pre.next;
pre.next = cur;
cur = next;
}
return sortedlisthead.next;
}